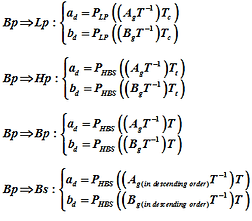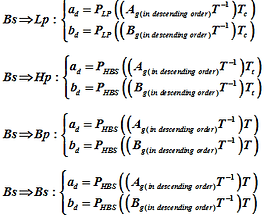Analog to Digiltal Filter Transformation
A digital filter (low pass, high pass, band pass and band stop) of the transfer function H(z) can be obtained from the transfer function H(s) of an designed analog filter as the block diagram shows below. The procedure of this method is first by transforming an analog filter (low pass, high pass, band pass, band stop, narrow band) into analog low pass prototype using Inverting Pascal matrix equations and then transforming into a desired digital filter using Analog to digital filter Pascal matrix eqaution.
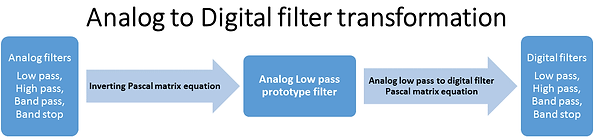
From the block diagram, an matrix equation can be derived called "Analog to Digital filter Pascal matrix equation" as written below
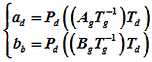
Analog Low pass to Digital filters
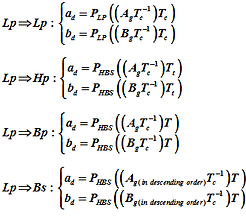
Analog High pass to Digital filters
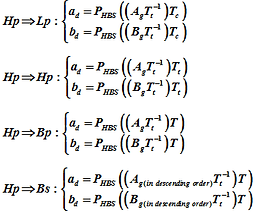
Analog Band pass to Digital filters
Analog Band stop to Digital filters