Frequeny transform in analog domin and digital domain
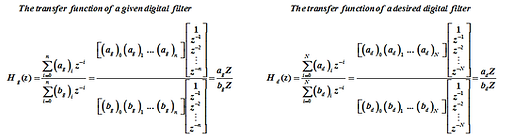
The frequency transformation may be used in analog domain or digital domain by maththematically mapping a designed filter into another filter which is meeting the desired specifications. Let H(s) denotes for the transfer function of an analog filter and H(z) is the transfer function of a digital filter, letters ‘A’ and ‘B’ are represented for the coefficient matrices in numerator and denominator of an analog filter, and similar for digital filter the letters ‘a’ and ‘b’ are used. The subscript ‘g’ denotes for ‘given’ and ‘d’ for ‘desired’.
The transfer function of a given and desired analog filter
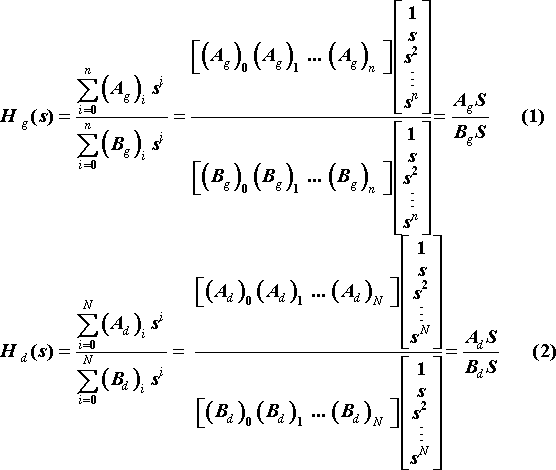
The transfer function of a given and desired digital filter
Frequency Transformation in s-domain
Frequency transformation in s-domain is a method to transform from a designed anlog filter into a different type of analog filter (low pass, high pass, band pass, band stop...). From the table I, there are two ways of transformation, transforming an analog low pass prototype in to an analog filter and transforming any type of analog filter into another analog filter. And form that, two matrix equations are derived, called "Analog low pass prototype to analog Pascal matrix equation" and "Analog to analog Pascal matrix equation".

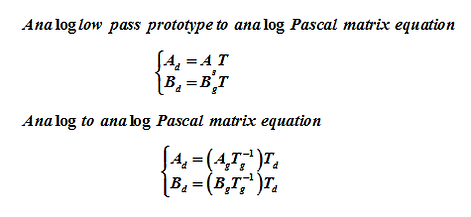
Frequency Transformation from s-domain to z-domain
Digital filters can be designed from an analog filter by uisng frequency transformation in s-domain and bililear z-transformation with pre-warping frequency as shown in table II below. The transfer function H(z) of a desired digital filter can be obtained form the transfer function H(s) of an analog low pass protoptye by using "Analog low pass prototype to analog Pascal matrix equation " or from any analog filter by using "Analog to analog Pascal matrix equation".

Frequency Transformation in z-domain
Frequency tranformation in z-domain using Digital to digital Pascal matrix equation is a new method to tranform any type of digital filters such as low pass, high pass, band pass, band stop into another digital filter. The involving of the Pascal’s triangle uses in the Pascal matrix equations made the work easier for hand-calculation and computing when transforming in z-domain. The features of the matrix [P] and [T] are so helpful to find the inverse matrix which are not easy to do with the larger matrix size. The algorithm of this method converse and inverse is so simple due to all operations imply the matrix multiplication and so it is more effective to program and calculation.

